Otsingud, diagrammid, statistika ja pöördtabelid

Olles läbi vaadanud põhifunktsioonid, raku viited ja kuupäeva- ja kellaajafunktsioonid, sukeldame nüüd mõningaid Microsoft Exceli täiustatud funktsioone. Esitame meetodeid klassikaliste finants-, müügiaruannete, veokulude ja statistika probleemide lahendamiseks.

KOOLI NAVIGATSIOON

1. Miks vajate valemeid ja funktsioone?
2. Valemi määratlemine ja loomine
3. Suhteline ja absoluutne raku viide ja vormindamine
4. Kasulikud funktsioonid, mida peaksite tundma õppima
5. Otsingud, diagrammid, statistika ja pöördtabelid

Need funktsioonid on ettevõtetele, üliõpilastele ja neile, kes lihtsalt tahavad rohkem teada saada, olulised.

VLOOKUP ja HLOOKUP

Siin on näide vertikaalse otsingu (VLOOKUP) ja horisontaalse otsingu (HLOOKUP) funktsioonide illustreerimiseks. Neid funktsioone kasutatakse numbri või muu väärtuse tõlkimiseks arusaadavaks. Näiteks saate kasutada VLOOKUP-i, et võtta osa number ja tagastada objekti kirjeldus.

Selle uurimiseks pöörduge tagasi meie 4. osa „Otsuste tegija” arvutustabelisse, kus Jane püüab otsustada, mida kanda kanda. Ta ei ole enam huvitatud sellest, mida ta kannab, sest ta on maandanud uue poisi, nii et ta kannab nüüd juhuslikke riideid ja kingi.

Jane'i arvutustabelis loetleb ta varustus vertikaalsetesse veergudesse ja kingadesse, horisontaalsetesse veergudesse.

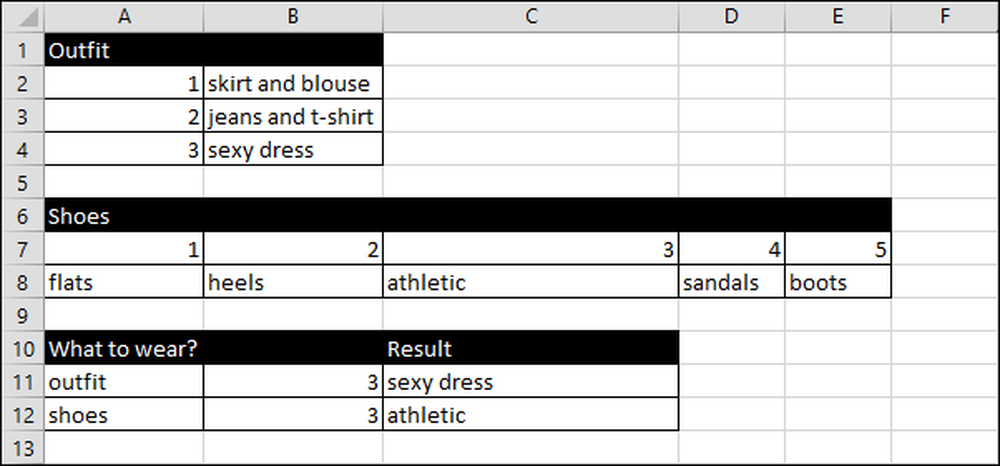
Ta avab arvutustabeli ja funktsioon RANDBETWEEN (1,3) genereerib numbri, mis on üks või kolm, mis vastab kolme tüüpi varustusele, mida ta saab kanda.

Ta kasutab funktsiooni RANDBETWEEN (1,5), et valida viie tüüpi kingade hulgast.

Kuna Jane ei saa kanda numbrit, siis peame selle nimeks teisendama, seega kasutame otsingufunktsioone.

Me kasutame VLOOKUP funktsiooni, et tõlkida riietuse number varustusnimeks. HLOOKUP tõlgib kinga numbrist rida erinevatele kingatüüpidele.

Arvutustabel toimib nii nagu varustus:

Excel valib juhusliku numbri ühest kolmest, sest tal on kolm varustusvalikut.

Järgnevalt teisendab valem valemiks tekstiks, kasutades = VLOOKUP (B11, A2: B4,2), mis kasutab juhuslikku arvu B11 väärtusest, et vaadata vahemikku A2: B4. Seejärel annab see tulemuse (C11) teises veerus loetletud andmetest.

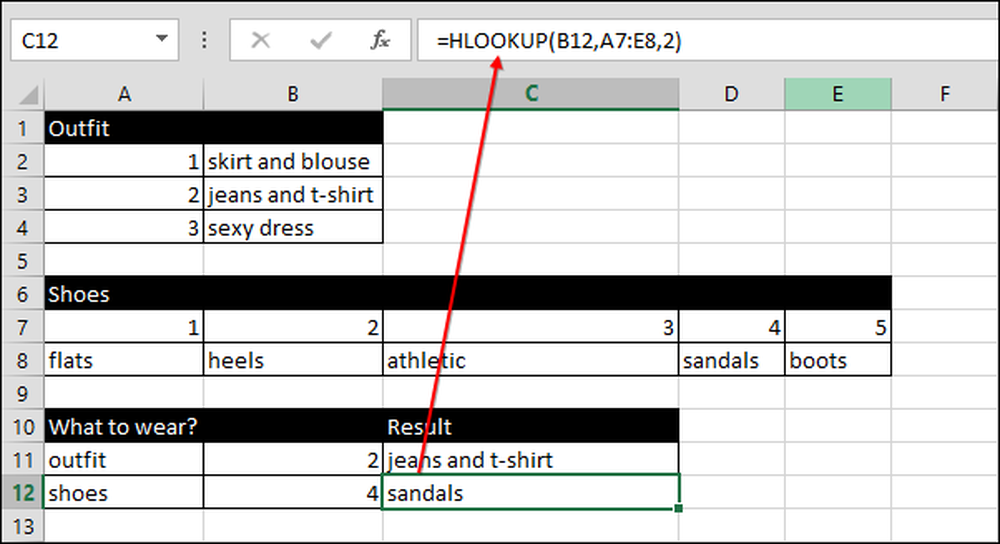
Me kasutame sama tehnikat kingade valimiseks, välja arvatud seekord, kui kasutame HLOOKUP asemel VOOKUP-i.

Näide: põhistatistika

Peaaegu igaüks teab statistikast ühte valemit - keskmine - kuid on veel üks äri jaoks oluline statistika: standardhälve.

Näiteks on paljud kolledžisse läinud inimesed oma SAT skoori üle agoniseerinud. Nad võiksid soovida teada, kuidas nad teiste õpilastega võrreldes auastmed on. Ülikoolid tahavad seda ka teada saada, sest paljud ülikoolid, eriti mainekad ülikoolid, vähendavad madala SAT-skooriga õpilasi.

Niisiis, kuidas me või ülikool mõõdaks ja tõlgendaks SAT tulemusi? Allpool on SAT-tulemused viie õpilase kohta, ulatudes 1870–2308 inimeseni.

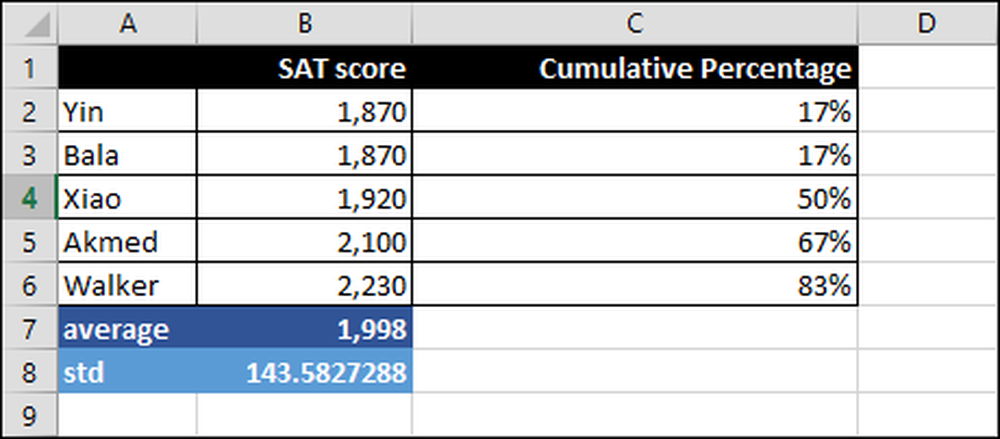
Olulised mõistetavad numbrid on:

Keskmine - Keskmist nimetatakse ka kui „keskmine”.

Standardhälve (STD või σ) - See number näitab, kui laialdaselt on hulk numbreid. Kui standardhälve on suur, siis numbrid on kaugel ja kui see on null, siis kõik numbrid on samad. Võiks öelda, et standardhälve on keskmine väärtus keskmise väärtuse ja täheldatud väärtuse vahel, st 1,998 ja iga SAT-skoor. Pange tähele, et tavaline on standardhälbe lühendamine kreeka sümboli sigma “σ” abil.

Protsentuaalne positsioon - Kui üliõpilane saab kõrgema skoori, saavad nad kallistada, et nad on tipptasemel 99 protsentiilil või midagi sellist. „Protsentuaalne auaste” tähendab, et skooride protsent on väiksem kui üks konkreetne tulemus.

Standardhälve ja tõenäosus on tihedalt seotud. Võid öelda, et iga standardhälbe puhul on tõenäosus või tõenäosus, et see arv on standardhälvete arvu sees:

STD	Tulemuste protsent	SAT-tulemuste vahemik
1	68%	1,854-2,142
2	95%	1,711-2,285
3	99,73%	1,567-2,429
4	99,994%	1,424-2,572

Nagu näete, on võimalus, et SAT-skoor on väljaspool 3 STD-d, praktiliselt null, sest 99,73 protsenti skooridest on 3 STD-s.

Nüüd vaatame uuesti arvutustabelit ja selgitage, kuidas see toimib.

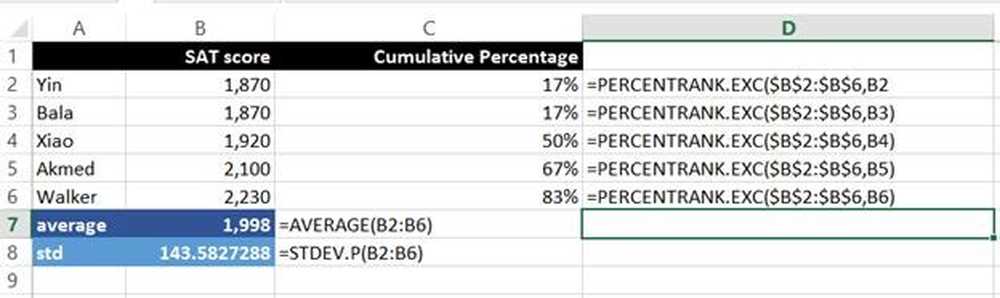
Nüüd selgitame valemid:

= AVERAGE (B2: B6)

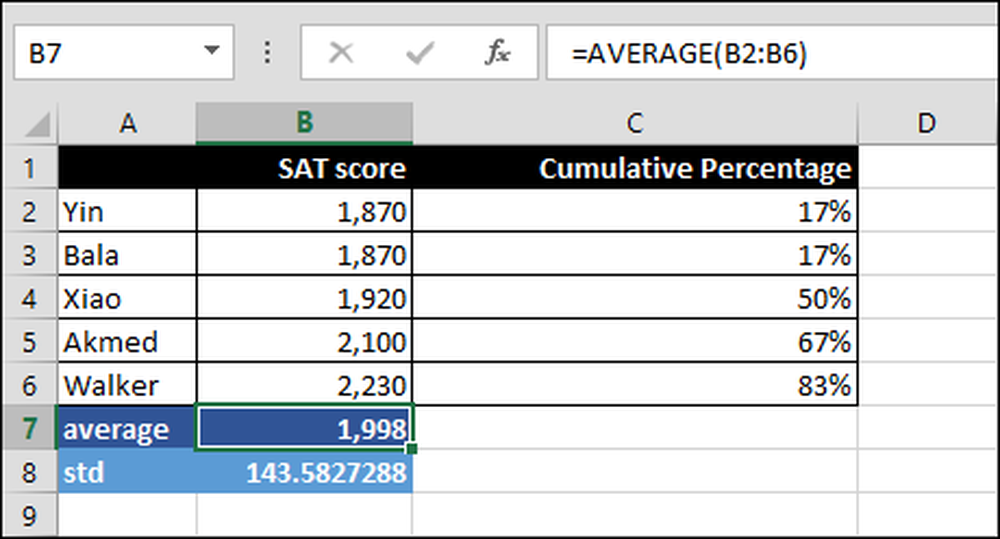
Kõikide tulemuste keskmine vahemikus B2: B6. Täpsemalt, kõigi skooride summa jagatud testi läbinud inimeste arvuga.

= STDEV.P (B2: B6)

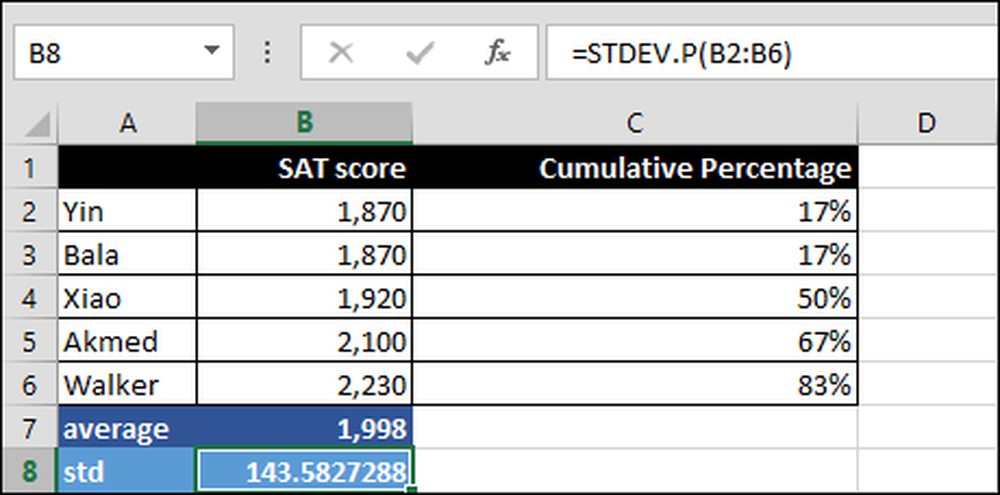
Standardhälve vahemikus B2: B6. “.P” tähendab STDEV.P-d, mida kasutatakse kõigi skooride, st kogu populatsiooni ja mitte ainult alamhulga üle..

= PERCENTRANK.EXC ($ B $ 2: $ B $ 6, B2)

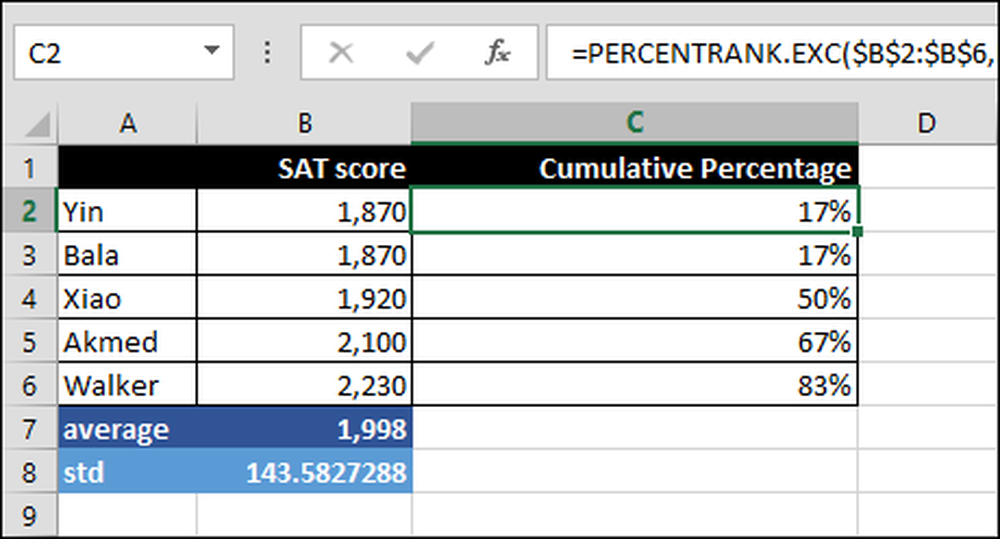
See arvutab kumulatiivse protsendi vahemikus B2: B6, mis põhineb SAT skooril, antud juhul B2. Näiteks 83 protsenti skooridest on Walkeri skoorist madalam.

Tulemuste graafik

Tulemuste graafikule viimine lihtsustab tulemuste mõistmist, lisaks saate selle esitluses näidata, et muuta oma punkt selgemaks.

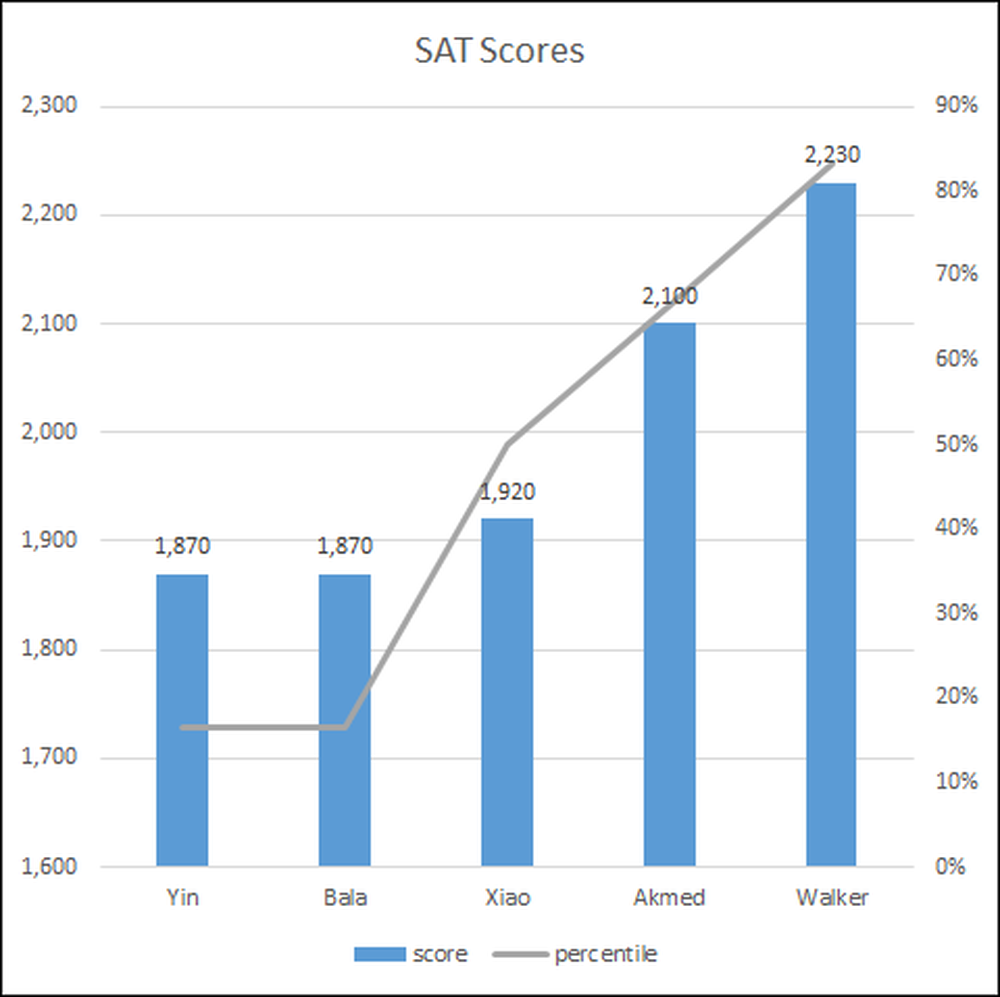
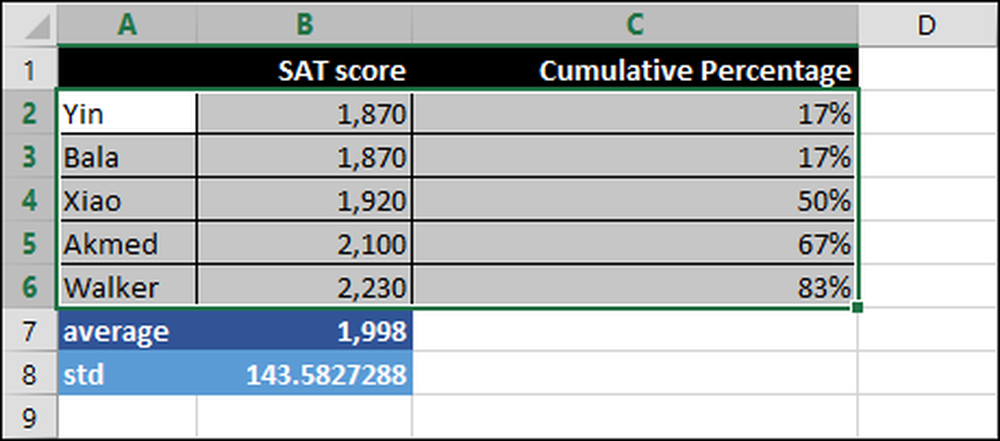
Õpilased asuvad horisontaalteljel ja nende SAT-tulemused on näidatud sinise ribadiagrammina skaalal (vertikaalteljel) 1600 kuni 2300.

Protsentiilide järjestus on parempoolne vertikaaltelg 0 kuni 90 protsenti ning seda kujutab hall joon.

Diagrammi loomine

Diagrammi loomine on ise teema, kuid selgitame lühidalt, kuidas ülaltoodud tabel loodi.

Kõigepealt valige graafikus olevate lahtrite hulk. Sel juhul A2 kuni C6, sest me tahame nii numbreid kui ka õpilaste nimesid.

Menüüst “Insert” valige „Charts” -> “Recommended Charts”:

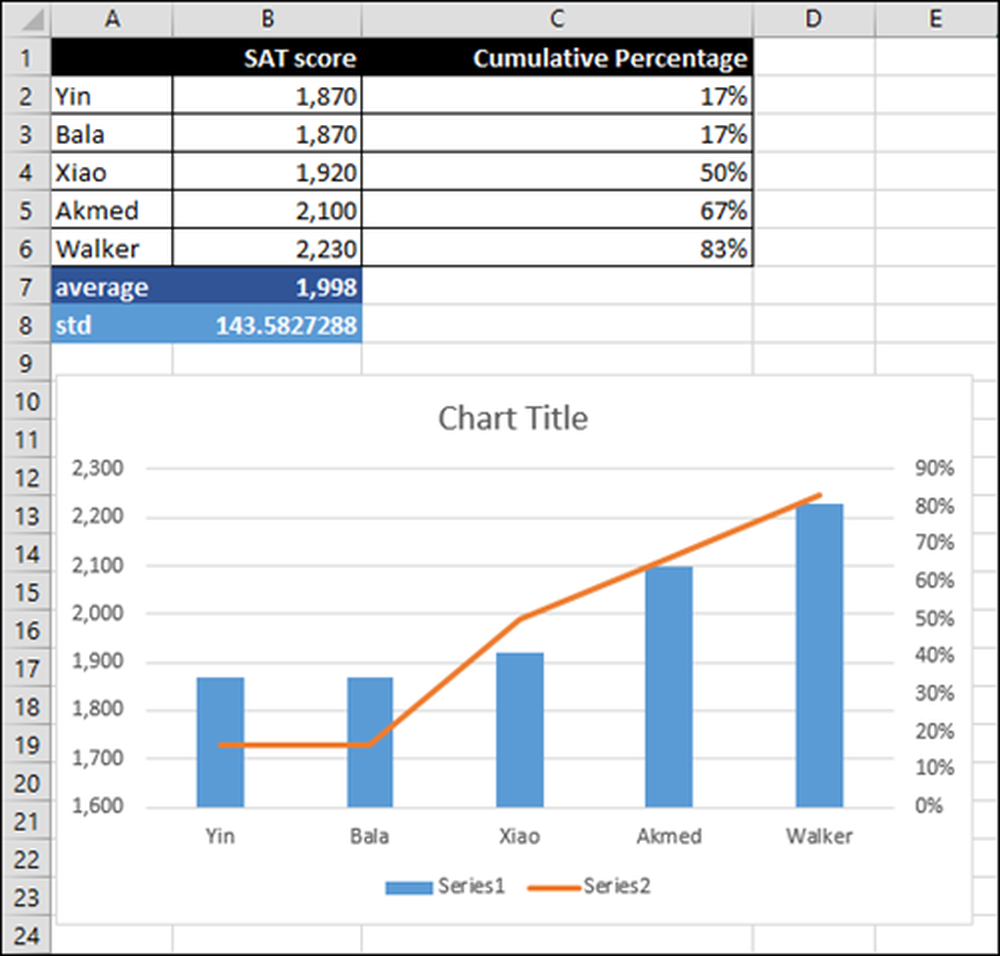
Arvuti soovitab diagrammi “Klastrite-kolonn, sekundaartelg”. "Sekundaartelje" osa tähendab, et see tõmbab kaks vertikaalset telge. Sel juhul on see diagramm see, mida me tahame. Me ei pea midagi muud tegema.

Võite kasutada diagrammi ümberpaigutamist ja suuruse muutmist seni, kuni teil on soovitud suurus ja asukoht. Kui olete rahul, saate diagrammi tabelisse salvestada.

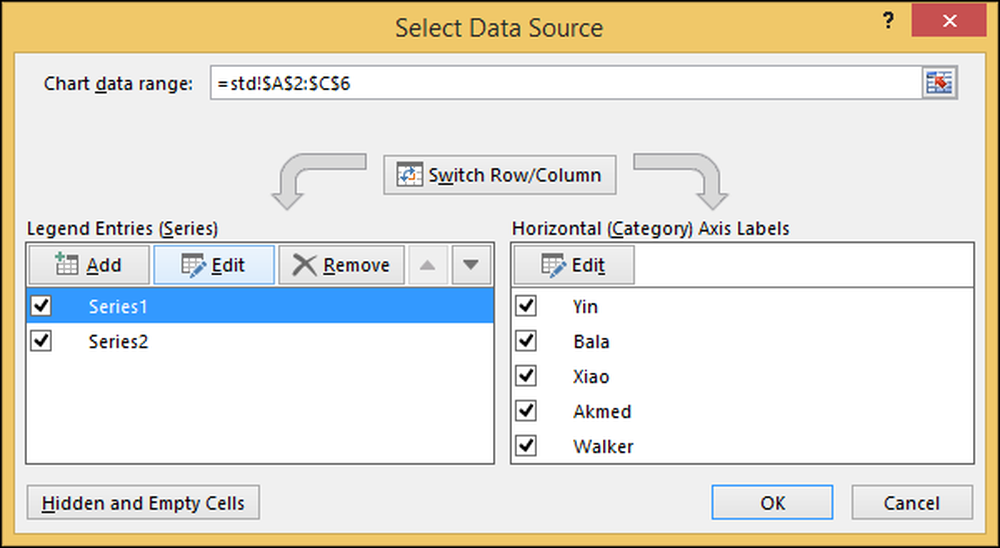
Kui paremklõpsate diagrammil, siis “Select Data”, näitab see, millised andmed on vahemiku jaoks valitud.

Funktsioon „Soovitatavad diagrammid” loob teid tavaliselt selliste keeruliste üksikasjadega tegelemisest, mis määravad, milliseid andmeid lisada, kuidas märgiseid määrata ja kuidas määrata vasakule ja paremale vertikaalset telge.

Dialoogis „Vali andmeallikas“ klõpsake „Leitud” (“Legend Entries” (seeria) ”all ja vajuta“ Edit ”ning muutke seda, et öelda“ Score ”.

Seejärel muutke 2. seeria (“protsentiil”) väärtuseks “Percentile”.

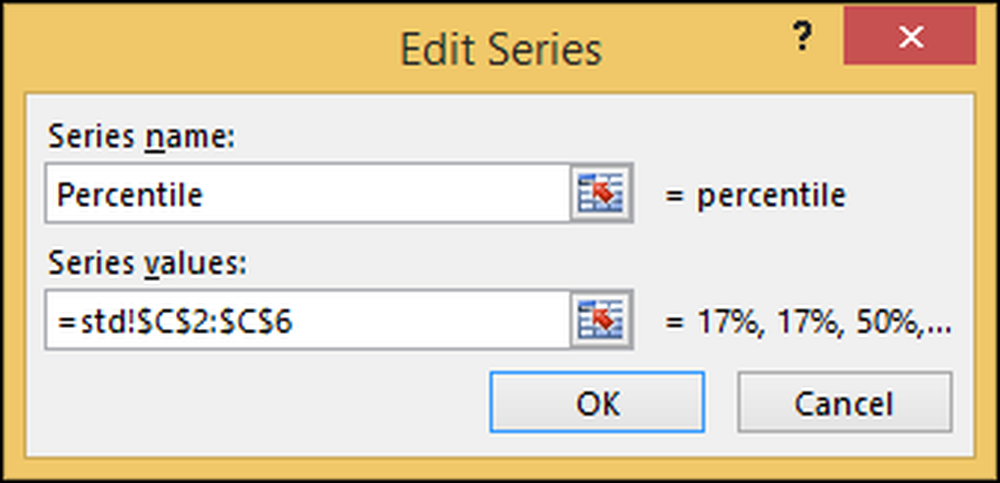
Tagasi oma diagrammi juurde ja klõpsa diagrammi pealkirjale ja muutke see „SAT-skooriks”. Nüüd on meil täielik skeem. Sellel on kaks horisontaaltelge: üks SAT skoori jaoks (sinine) ja üks kumulatiivse protsendi jaoks (oranž).

Näide: transpordiprobleem

Transpordiprobleem on klassikaline näide matemaatika tüübist, mida nimetatakse lineaarseks programmeerimiseks. See võimaldab teil maksimeerida või vähendada teatud piirangutega seotud väärtust. Sellel on palju rakendusi, mis pakuvad laia valikut äriprobleeme, seega on kasulik teada, kuidas see toimib.

Enne selle näite alustamist peame lubama „Excel Solveri”.

Luba Solveri lisandmoodul

Valige “File” -> “Options” -> “Add-ins”. Lisandmoodulite allosas klõpsake nupul „Halda: Exceli lisandmoodulid“ asuvat nuppu „Mine”.

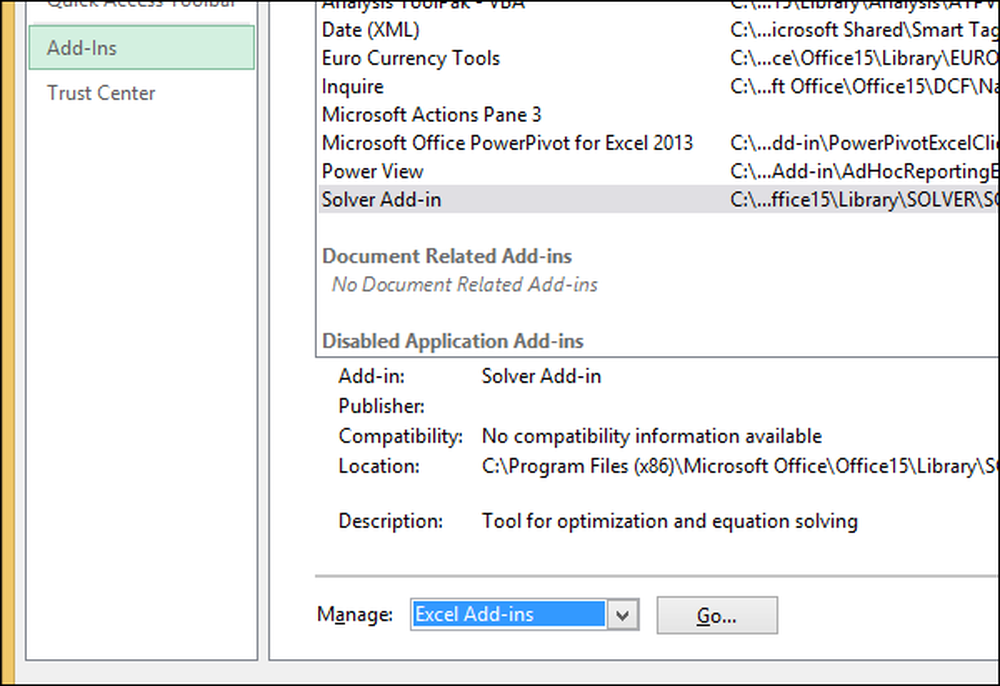
Klõpsake tulemuseks olevas menüüs märkeruutu, et lubada, “Solver Add-in” ja klõpsa „OK“.

Näide: Arvuta madalaimad iPadi tarnekulud

Oletame, et me tarnime iPade ja püüame täita oma jaotuskeskusi, kasutades kõige väiksemaid transpordikulusid. Meil on kokkulepe transpordi- ja lennufirma vahel, et saata iPadid Shanghai, Pekingi ja Hongkongi vahel allpool näidatud jaotuskeskustesse.

Iga iPadi saatmise hind on tehasest kuni jaotuskeskuseni jõudmise jaamani jagamine 20 000 kilomeetriga. Näiteks on see 8244 km kaugusel Shanghaist Melbourne'i, mis on 8 024/20 000 või 0,40 dollarit iPadi kohta.

Küsimus on selles, kuidas saame kõik need iPadid nendelt kolmetelt tehastelt nelja sihtpunkti saata võimalikult väikeste kuludega?

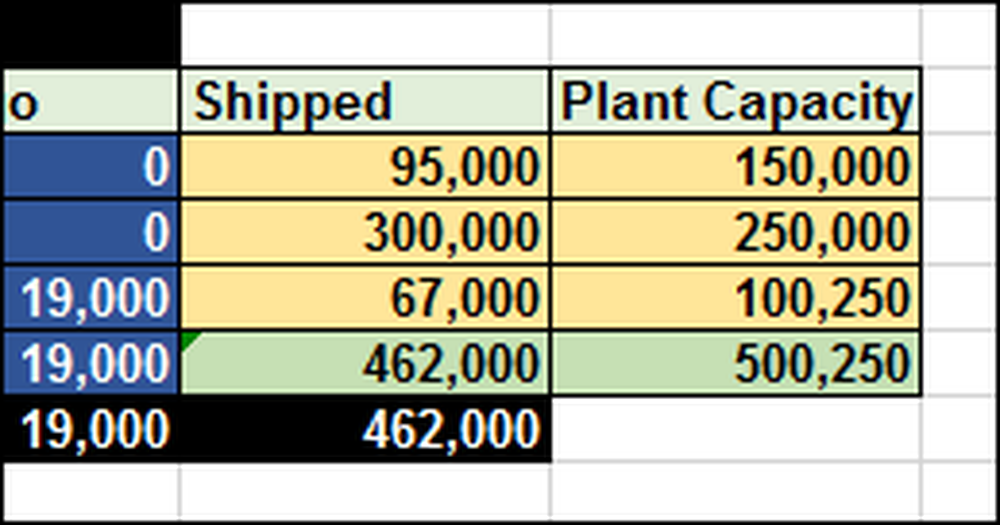
Nagu võite ette kujutada, võib see olla väga raske ilma igasuguse valemi ja vahendita. Sellisel juhul peame saatma 462 000 (F12) iPadi. Taimedel on piiratud võimsus 500 250 (G12) ühikut.

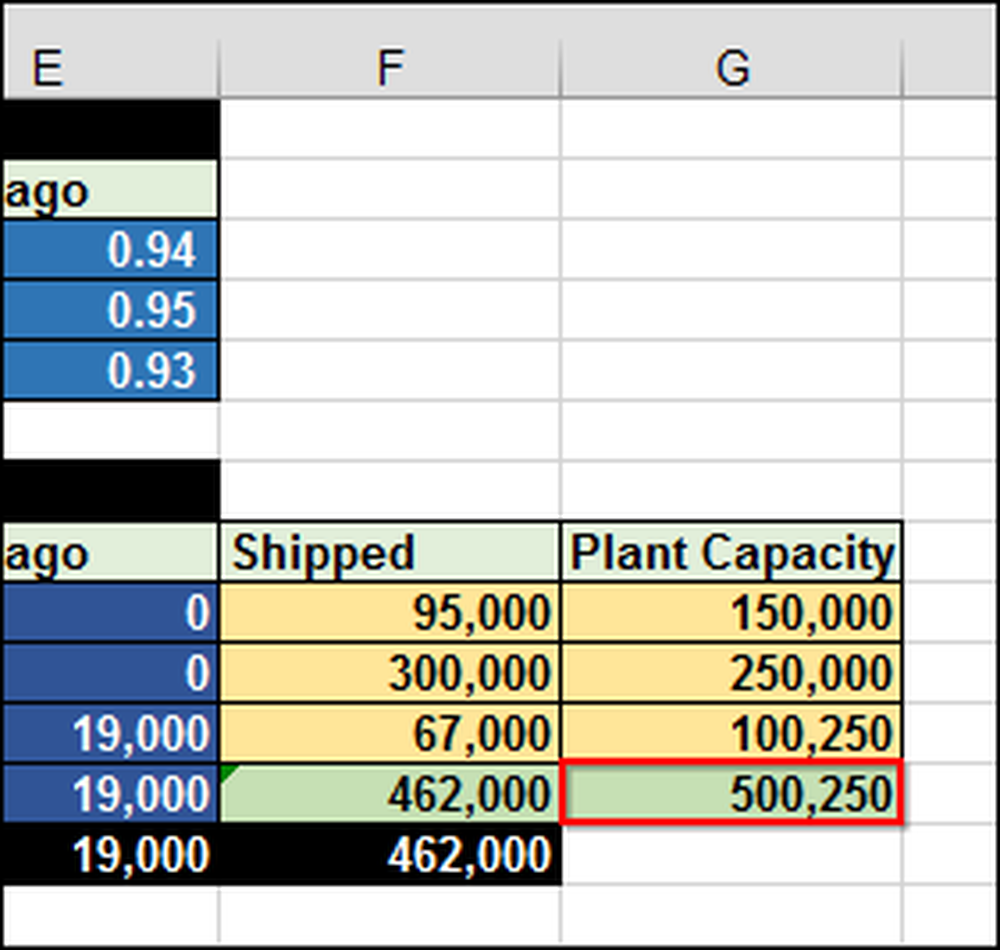
Arvutustabelis, et saaksite näha, kuidas see toimib, oleme kirjutanud 1 lahtrisse B10, mis tähendab, et tahame saata ühe iPadi Shanghaist Melbourne'i. Kuna transpordikulud sellel marsruudil on $ 0,40 iPadi kohta, on kogumaksumus (B17) 0,40 dollarit.

Arv arvutati funktsiooni = SUMPRODUCT (kulud, tarnitud) „kulud” alusel vahemikus B3: E5.

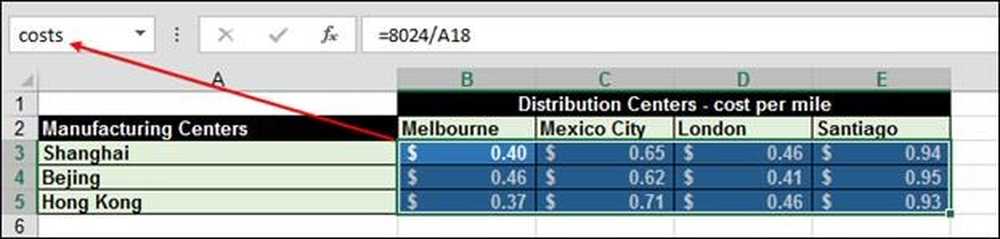
Ja “saadetakse” on vahemik B9: E11:

SUMPRODUCT korrutab “kulud” korda “tarnitud” (B14). Seda nimetatakse "maatriksi korrutamiseks".

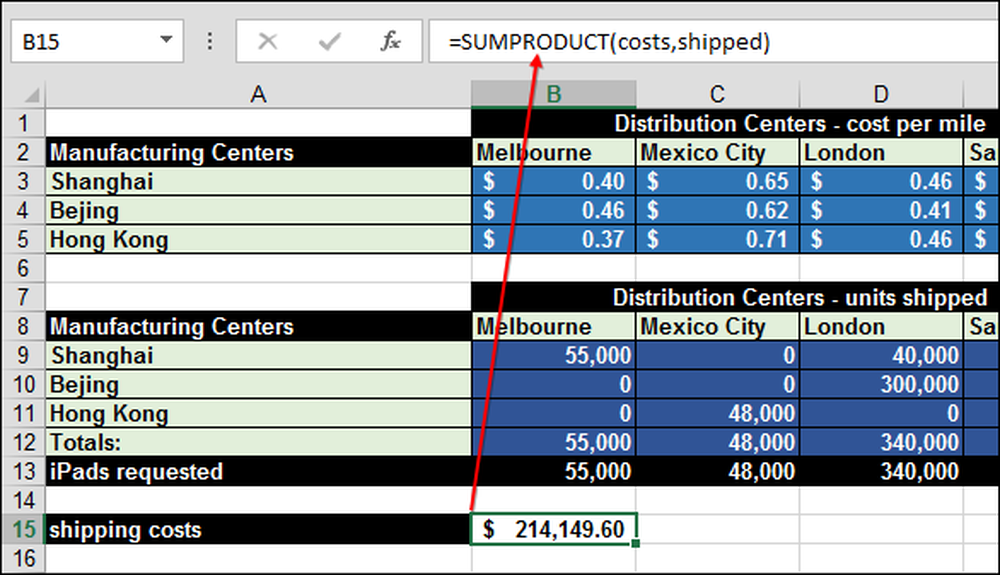
Selleks, et SUMPRODUCT toimiks korralikult, peavad need kaks maatriksit - kulud ja saadetised - olema sama suurusega. Sellest piirangust saate saada lisakulusid ja nullväärtusega veergude ja ridade saatmist, et massiivid oleksid sama suured ja ei mõjutaks kogukulusid.

Solveri kasutamine

Kui kõik, mida me pidime tegema, oli korrutada "kulusid" sisaldavaid maatriksid, mis ei ole liiga keerulised, kuid me peame tegelema ka sealsete piirangutega.

Me peame saatma, mida iga jaotuskeskus nõuab. Me paneme selle konstantse lahendisse sellesse: $ B $ 12: $ E $ 12> = $ B $ 13: $ E $ 13. See tähendab saadetavate summade summat, s.t. lahtrites $ B $ 12: $ E $ 12 olevad summad peavad olema suuremad või võrdsed sellega, mida iga jaotuskeskus nõuab ($ B $ 13: $ E $ 13).

Me ei saa saata rohkem kui me toodame. Kirjutame sellised piirangud nagu: $ F $ 9: $ F $ 11 <= $G$9:$G$11. Put another way, what we ship from each plant $F$9:$F$11 cannot exceed (must be less than or equal to) the capacity of each plant: $G$9:$G$11.

Nüüd mine menüüsse „Andmed“ ja vajutage nuppu „Solver”. Kui nupp "Solver" ei ole olemas, peate lubama Solveri lisandmooduli.

Sisestage kaks eelnevalt täpsustatud piirangut ja valige vahemik „Saadetised”, mis on arvude vahemik, mida me tahame, et Excel arvutaks. Samuti vali vaikimisi algoritm „Simplex LP” ja osuta sellele, et tahame lahtrit B15 „minimeerida” (“kogumaksumus”), kus see ütleb “Set Objective”.

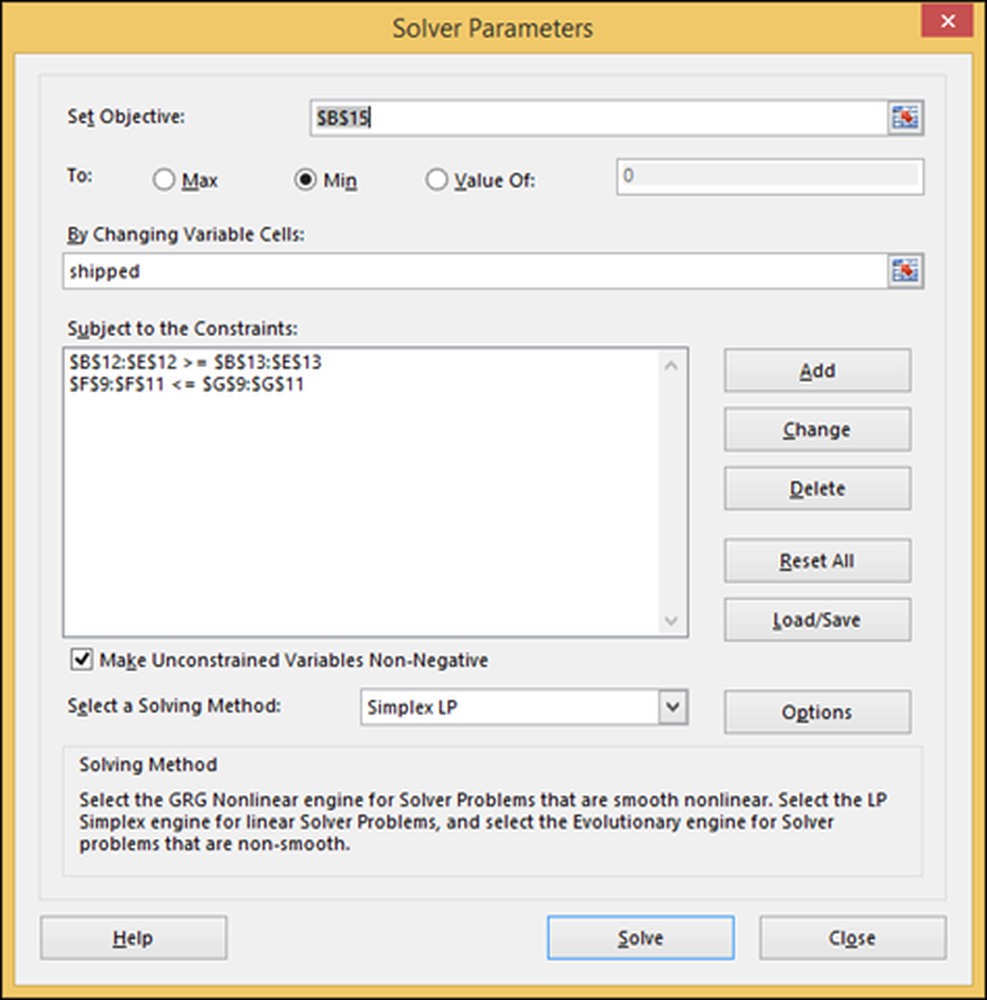
Vajutage „Lahenda“ ja Excel salvestab tulemused arvutustabelisse, mida me tahame. Samuti saate selle salvestada, et saaksite teiste stsenaariumidega mängida.

Kui arvuti ütleb, et ei leia lahendust, siis olete teinud midagi, mis ei ole loogiline, näiteks olete võib-olla taotlenud rohkem iPade, kui taimed võivad toota.

Siin ütleb Excel, et leidis lahenduse. Lahuse hoidmiseks ja arvutustabelisse naasmiseks vajutage „OK“.

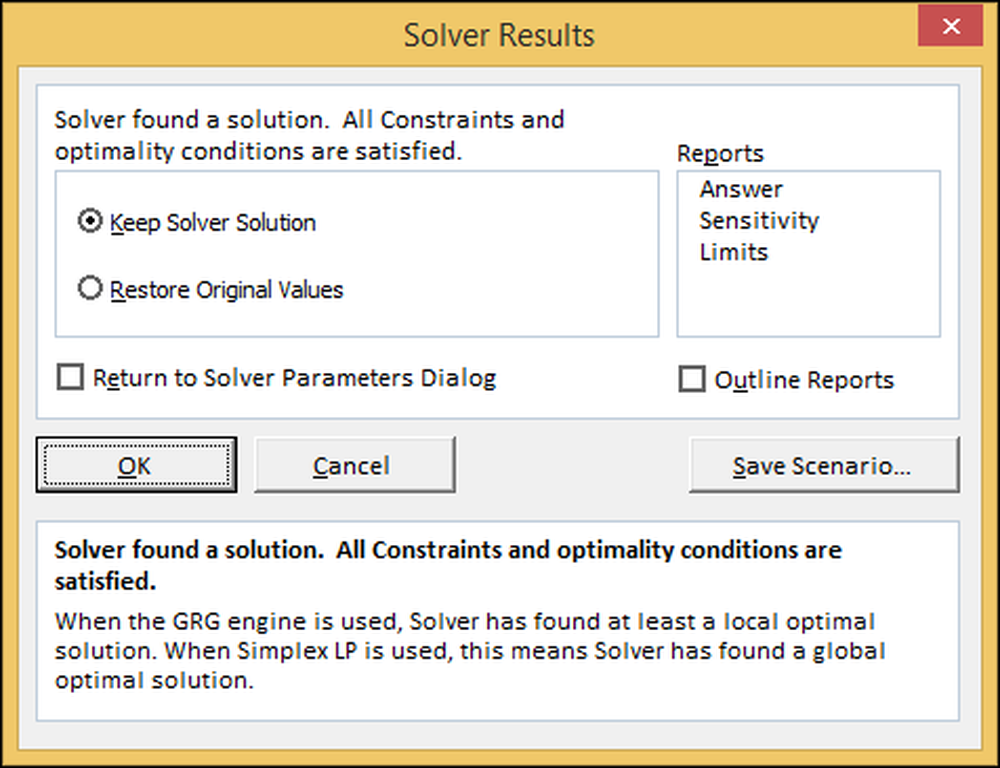
Näide: nüüdisväärtus

Kuidas otsustab ettevõte, kas investeerida uude projekti? Kui „netoväärtus” on positiivne, investeerivad nad sellesse. See on enamiku finantsanalüütikute tavapärane lähenemisviis.

Oletame näiteks, et Codelco kaevandusettevõte tahab laiendada Andinase vaskkaevu. Standardmeetod, mille alusel otsustatakse, kas projektiga edasi liikuda, on nüüdisväärtuse arvutamine. Kui NPV on suurem kui null, siis on projekt kasumlik, arvestades kahte sisendit (1) ja (2) kapitali hinda.

Inglise keeles tähendab kapitali maksumus seda, kui palju see raha teeniks, kui nad lihtsalt pangast lahkuksid. Kasutate kapitali maksumust, et diskonteerida raha väärtusi praegusele väärtusele, teisisõnu võib $ 100 viie aasta jooksul olla 80 dollarit.

Esimesel aastal eraldatakse projekti rahastamiseks kapitalina 45 miljonit dollarit. Raamatupidajad on otsustanud, et nende kapitali maksumus on kuus protsenti.

Kui nad hakkavad kaevandamist alustama, hakkab raha tulema, kui ettevõte leiab ja müüb toodetud vaske. Loomulikult, mida rohkem nad kaevandavad, seda rohkem raha nad teevad ja nende prognoos näitab, et nende rahavoog suureneb, kuni see jõuab 9 miljoni dollarini aastas.

Pärast 13 aastat on NPV $ 3,945,074 USD, seega on projekt kasumlik. Finantsanalüütikute hinnangul on „tasuvusaeg” 13 aastat.

Pivot tabeli loomine

„Pivot table” on põhimõtteliselt raport. Me nimetame neid pivot-tabeleideks, sest saate hõlpsasti vahetada neid ühe tüüpi aruandega teisele, ilma et peaksite kogu uue aruande koostama. Nii nad pivot kohas. Näitame põhinäidet, mis õpetab põhilisi mõisteid.

Näide: müügiaruanded

Müügipersonal on väga konkurentsivõimeline (see on osa müügimeest), nii et nad soovivad loomulikult teada, kuidas nad kvartali lõpus ja aasta lõpus üksteise vastu maksavad, ning kui palju on nende komisjonitasud..

Oletame, et meil on kolm müügimeest - Carlos, Fred ja Julie - kõik müüvad naftat. Nende müük dollarites 2014. aasta eelarve kvartali kohta on toodud allpool tabelis.

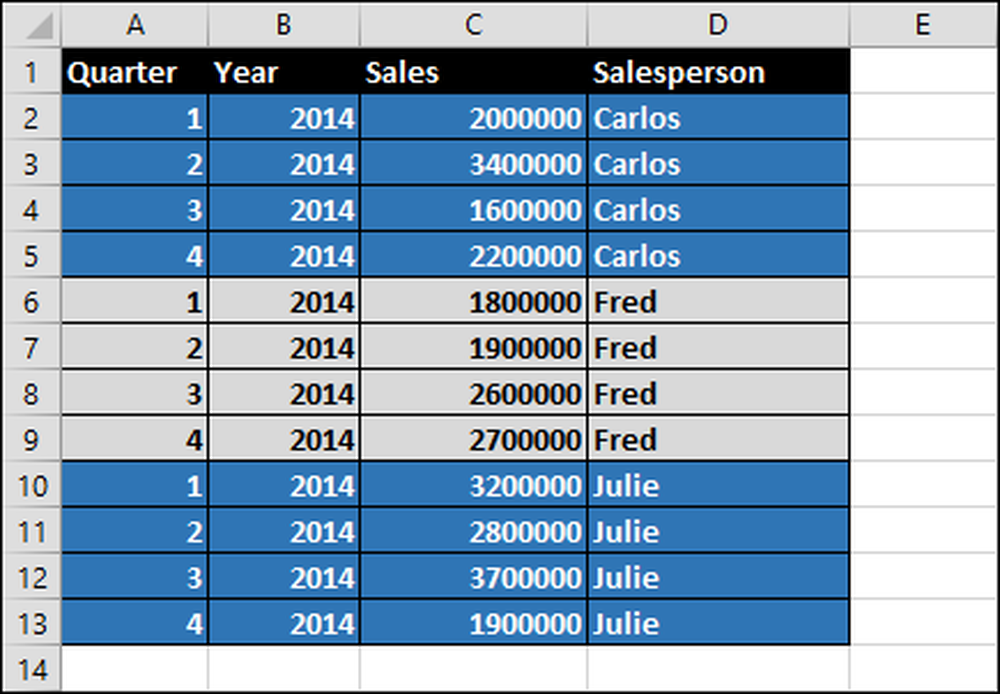
Nende aruannete koostamiseks loome pivot tabeli:

Valige „Insert -> Pivot Table”, mis asub tööriistariba vasakus servas:

Valige kõik read ja veerud (sh müügimehe nimi), nagu allpool näidatud:

Pöördtabeli dialoogiboks kuvatakse arvutustabeli paremal küljel.

Kui klõpsame kõigil neljal väljal tabeli dialoogiaknas (kvartal, aasta, müük ja müüja), lisab Excel arvutustabelisse aruande, millel pole mõtet, aga miks?

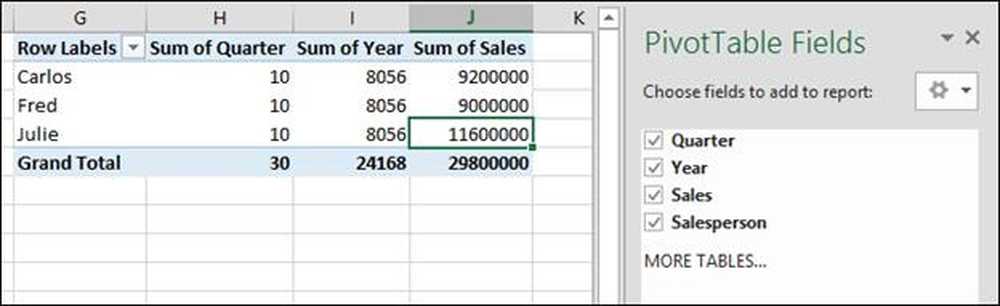
Nagu näete, oleme valinud kõik aruandele lisatavad neli välja. Exceli vaikekäitumine on rühmitada ridu tekstiväljade kaupa ja seejärel kokku ülejäänud read.

Siin antakse meile aasta 2014 + 2014 + 2014 + 2014 = 24 168 summa, mis on mõttetu. Samuti andis see kvartalite 1 + 2 + 3 + 4 = 10 * 3 = 3 0 summa. Me ei vaja seda teavet, nii et me eemaldame need väljad, et eemaldada need meie pivot-tabelist.

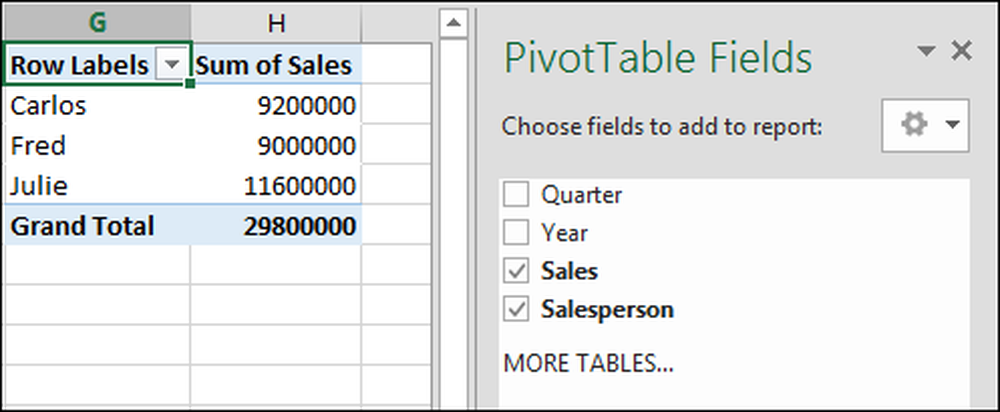
„Müügi summa” (kogumüük) on siiski asjakohane, nii et me selle lahendame.

Näide: Müüja müük

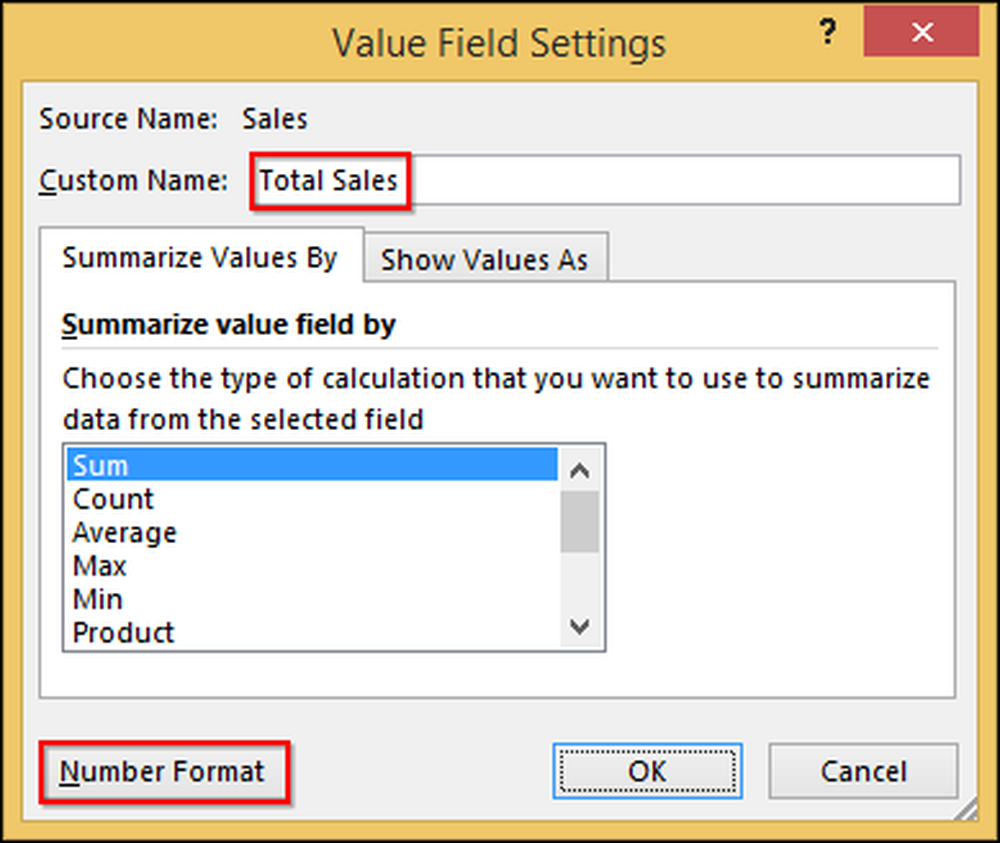
Saate redigeerida „Müügi summat”, mis on selgem kui „Kokku müük”. Samuti saate vormindada rakke valuuta kujul, nagu te vormindaksite teisi rakke. Kõigepealt klõpsake „Müügisumma” ja valige „Väärtuse väljad”.

Saadud dialoogis muudame nime “Total Sales”, seejärel klikkige “Number Format” ja muutke see “Valuutaks”.

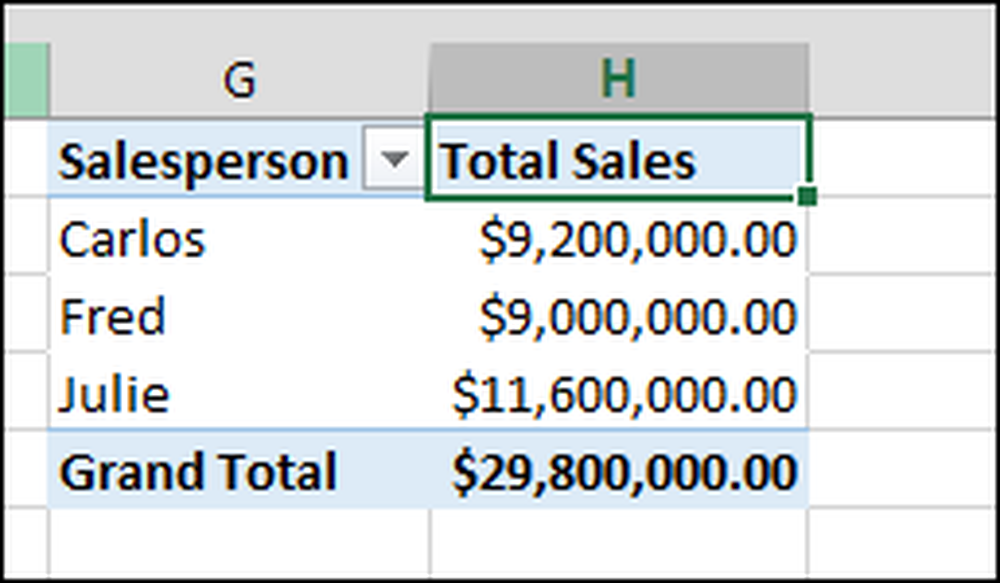
Seejärel näete oma käetööd pivot tabelis:

Näide: Müüja ja kvartali müük

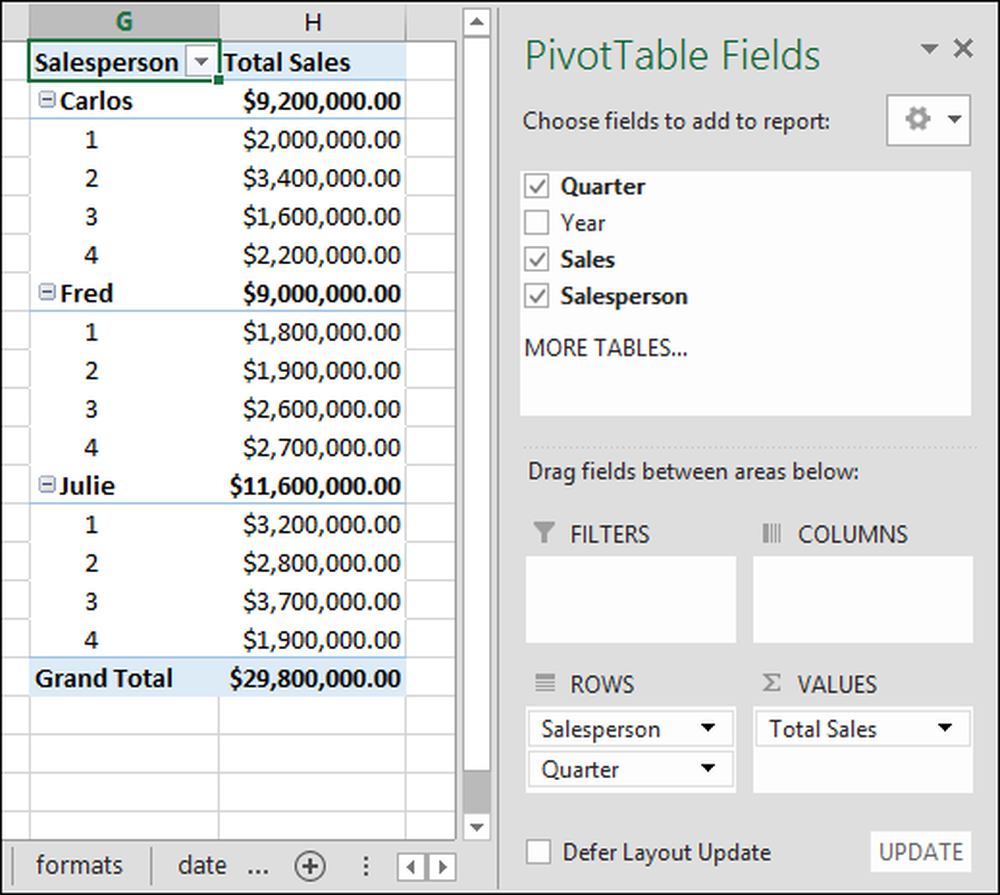
Nüüd lisame iga kvartali vahesummad. Vahesummade lisamiseks klõpsa hiire vasakult klõpsuga väljale „Quarter” ja hoidke ja lohistage see “ridade” sektsiooni. Saate näha tulemust alloleval pildil:

Kui me selle juures oleme, eemaldagem „kvartali summa” väärtused. Lihtsalt klõpsake noolel ja klõpsake „Eemalda väli“. Ekraanil näete nüüd, et oleme lisanud “Kvartali” read, mis jagavad iga müüja müügi kvartalite kaupa.

Neid oskusi silmas pidades saate nüüd oma andmetest luua tabelid!

Järeldus

Pakkudes oleme näidanud teile mõningaid Microsoft Exceli valemite ja funktsioonide funktsioone, mida saate Microsoft Exceli oma äri-, akadeemiliste või muude vajaduste jaoks rakendada.

Nagu olete näinud, on Microsoft Excel tohutu toode, millel on nii palju funktsioone, et enamik inimesi, isegi arenenud kasutajad, ei tea neid kõiki. Mõned inimesed võivad öelda, et see muudab selle keeruliseks; tunneme, et see on põhjalikum.

Loodetavasti oleme palju reaalseid näiteid esitades näidanud mitte ainult Microsoft Exceli funktsioone, vaid õpetanud teile midagi statistikast, lineaarsest programmeerimisest, diagrammide loomisest, juhuslike numbrite ja muude ideede abil, mida saate nüüd vastu võtta ja kasutada oma koolis või kus te töötate.

Pidage meeles, et kui tahad uuesti klassi tagasi minna, saate värskelt alustada 1. õppetundiga!